Vrsta lekcije: postavljanje zadatka za učenje.
Ciljevi lekcije:
Obrazovni: sistematizirati znanje učenika o metodama rješavanja jednostavnih trigonometrijskih jednačina, učvrstiti vještine rada sa kružićima i tabelama.
Razvojni: nastaviti rad na formiranju kreativnih intelektualnih sposobnosti učenika korištenjem različitih tehnika rješavanja trigonometrijskih jednačina.
Obrazovni: razvijati vještine kolektivne mentalne aktivnosti, međusobne podrške i prihvaćanja gledišta drugačijeg od vlastitog.
Tokom nastave
1. Situacija uspjeha.
Riješite jednačinu: cosx=1; cosx=0; cosx= -1.
2. Situacija, jaz” između znanja i neznanja.
Riješite jednačinu: cosx=½; cosx=a.
Diskusija.
3. Iskaz obrazovnog zadatka.
Kako riješiti jednačinu ovog tipa?
1) Kolika je apscisa tačke na jediničnom krugu dobijena rotacijom tačke (1;0) oko početka za ugao jednak: ?
2). Šta je jednako: 
?
odgovor:
3).Šta je jednako: .
odgovor:
;
;
(1)
.
Riječi nastavnika: matematičari su riječi reverse cos nazvali riječju arccosine (arccos). Lučni kosinus broja je broj čiji je kosinus jednak a:
arccosa=α, ako je cosα=a i 0≤α≤π.
4). Napišite jednakost (1) koristeći simbol arccos.
5). Riješite jednačine: cosx=½, cosx=α.
Odgovor: x=arccos½, x=arccosa.
6). Imenujte uglove rotacije tačke (1;0) jedinične kružnice koja ima apscisu jednaku ½.
Odgovor: apscisa je jednaka ½ kada se tačka rotira za ugao jednak π/3 i -π/3.
tj. cosx=½ na x=±arccos½
cosx=a na x=±arccosa.
7). Koje su apscise tačaka dobijenih rotacijom tačke (1;0) za uglove: π/3+2π; π/3+6π; -π/3+4π; -π/3+8π; π/3+2πn; -π/3+2πn.
Odgovor: apscisa je ½, a cosx=½ na x=±arccos½+2πn,.
cosx=a na x=±arccosa+2πn,.
8). Zaključak: jednačina cosx=a
1) ima korijen ako je ≤1,
2) nema korijena ako je >1.
9). Sažetak lekcije:
a) Za koje vrijednosti a i α jednakost arccosa = α ima smisla?
b) Šta se naziva arc kosinus od a?
c) Pri kojim vrijednostima a jednačina cosx=a ima korijen?
d) Formula za pronalaženje korijena jednačine cosx=a.
primjeri:
\(2\sin(x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2x+4\sinx-1=0\)
\(\cos4x+3\cos2x=1\)
Kako riješiti trigonometrijske jednadžbe:
Bilo koju trigonometrijsku jednačinu treba svesti na jedan od sljedećih tipova:
\(\sint=a\), \(\cost=a\), tg\(t=a\), ctg\(t=a\)
gdje je \(t\) izraz sa x, \(a\) je broj. Takve trigonometrijske jednačine su pozvani najjednostavniji. Mogu se lako riješiti korištenjem () ili posebnim formulama:
Pogledajte infografiku o rješavanju jednostavnih trigonometrijskih jednadžbi ovdje: i.
Primjer . Riješite trigonometrijsku jednačinu \(\sinx=-\)\(\frac(1)(2)\).Rješenje:
odgovor: \(\left[ \begin(sakupljeno)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(sakupljeno)\desno.\) \(k,n∈Z\)
Šta svaki simbol znači u formuli za korijene trigonometrijskih jednačina, pogledajte.
Pažnja! Jednačine \(\sinx=a\) i \(\cosx=a\) nemaju rješenja ako je \(a ϵ (-∞;-1)∪(1;∞)\). Zato što su sinus i kosinus za bilo koji x veći ili jednaki \(-1\) i manji ili jednaki \(1\):
\(-1≤\sin x≤1\) \(-1≤\cosx≤1\)
Primjer
. Riješite jednačinu \(\cosx=-1,1\).
Rješenje:
\(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Odgovori
: nema rješenja.
Primjer . Riješite trigonometrijsku jednačinu tg\(x=1\).
Rješenje:
|
|
Rešimo jednačinu pomoću brojevnog kruga. Za ovo: |
Primjer
. Riješite trigonometrijsku jednačinu \(\cos(3x+\frac(π)(4))=0\).
Rješenje:
|
|
Koristimo ponovo brojčani krug. \(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\) 8) Kao i obično, izrazit ćemo \(x\) u jednačinama. \(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) |
Svođenje trigonometrijskih jednadžbi na najjednostavnije je kreativan zadatak, ovdje morate koristiti obje i posebne metode za rješavanje jednačina:
- Metoda (najpopularnija u Jedinstvenom državnom ispitu).
- Metoda.
- Metoda pomoćnih argumenata.
Razmotrimo primjer rješavanja kvadratne trigonometrijske jednadžbe
Primjer . Riješite trigonometrijsku jednačinu \(2\cos^2x-5\cosx+2=0\)Rješenje:
|
\(2\cos^2x-5\cosx+2=0\) |
Napravimo zamjenu \(t=\cosx\). |
|
Naša jednačina je postala tipična. Možete ga riješiti pomoću . |
|
|
\(D=25-4 \cdot 2 \cdot 2=25-16=9\) |
|
|
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\) |
Vršimo obrnutu zamjenu. |
|
\(\cosx=\)\(\frac(1)(2)\); \(\cosx=2\) |
Prvu jednačinu rješavamo pomoću brojevnog kruga. |
 |
Zapišimo sve brojeve koji leže na ovim tačkama. |
Primjer rješavanja trigonometrijske jednadžbe sa proučavanjem ODZ-a:
Primjer (USE) . Riješite trigonometrijsku jednačinu \(=0\)|
\(\frac(2\cos^2x-\sin(2x))(ctg x)\)\(=0\) |
Postoji razlomak i postoji kotangens - to znači da ga trebamo zapisati. Da vas podsjetim da je kotangens zapravo razlomak: ctg\(x=\)\(\frac(\cosx)(\sinx)\) Prema tome, ODZ za ctg\(x\): \(\sinx≠0\). |
|
ODZ: ctg\(x ≠0\); \(\sinx≠0\)
\(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\) |
Označimo "ne-rješenja" na brojčanom krugu. |
|
\(\frac(2\cos^2x-\sin(2x))(ctg x)\)\(=0\) |
Oslobodimo se imenioca u jednadžbi tako što ćemo ga pomnožiti sa ctg\(x\). To možemo učiniti, jer smo gore napisali da je ctg\(x ≠0\). |
|
\(2\cos^2x-\sin(2x)=0\) |
Primijenimo formulu dvostrukog ugla za sinus: \(\sin(2x)=2\sinx\cosx\). |
|
\(2\cos^2x-2\sinx\cosx=0\) |
Ako vam se ruke ispruže da podijelite po kosinsu, povucite ih natrag! Možete podijeliti izrazom s promjenljivom ako ona definitivno nije jednaka nuli (na primjer, ove: \(x^2+1.5^x\)). Umjesto toga, uzmimo \(\cosx\) iz zagrada. |
|
\(\cosx (2\cosx-2\sinx)=0\) |
Hajde da "podelimo" jednačinu na dva. |
|
\(\cosx=0\); \(2\cosx-2\sinx=0\) |
Rešimo prvu jednačinu pomoću brojevnog kruga. Podijelimo drugu jednačinu sa \(2\) i pomjerimo \(\sinx\) na desnu stranu. |
 |
|
|
\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cosx=\sinx\) |
Dobiveni korijeni nisu uključeni u ODZ. Stoga ih nećemo zapisivati kao odgovor. |
|
Ponovo koristimo krug. |
|
|
|
Ove korijene ODZ ne isključuje, pa ih možete napisati u odgovoru. |
cos jednadžba X = A
Svaki korijen jednačine
cos X = A (1)
može se posmatrati kao apscisa neke presečne tačke sinusoide y = cosX sa pravom linijom y =A , i obrnuto, apscisa svake takve točke presjeka je jedan od korijena jednačine (1) Dakle, skup svih korijena jednačine (1) poklapa se sa skupom apscisa svih presječnih tačaka kosinusnog vala. y = cosX sa pravom linijom y = A .
Ako | A| >1 , zatim kosinus y = cosX ne seče pravom y = A .
U ovom slučaju, jednačina (1) nema korijen.
At |A| < 1 postoji beskonačno mnogo tačaka preseka.
za a > 0
za< 0.
Sve ove presečne tačke podelićemo u dve grupe:
A -2 , A - 1 , A 1 , A 2 , ... ,
B -2 , B - 1 , B 1 , B 2 , ... ,
Dot A ima apscisu arccos A , a sve ostale tačke prve grupe su odvojene od nje na udaljenostima koje su višestruke od 2 π
arccos a+ 2k π . (2)
Dot IN, kao što se može lako razumjeti iz slika, ima apscisu - arccosA , a sve ostale točke druge grupe uklanjaju se iz njega na udaljenostima koje su višestruke od 2 π . Stoga se njihove apscise izražavaju kao
arccos A+ 2nπ . (3)
Dakle, jednadžba (1) ima dvije grupe korijena definirane formulama (2) i (3). Ali ove dvije formule se očito mogu napisati kao jedna formula
X = ± arccos a+ 2m π , (4)
Gdje m prolazi kroz sve cijele brojeve (m = 0, ±1, ±2, ±3, ...).
Obrazloženje koje smo sproveli pri izvođenju ove formule ispravno je samo ako
| a| =/= 1. Međutim, formalno relacija (4)
određuje sve korijene jednačine cosx=a
i na | A| =1. (Dokažite!) Stoga možemo reći da je formula (4)
daje sve korijene jednadžbe (1) za bilo koje vrijednosti A
, Kad bi samo |A|
<
1
.
Ali ipak u tri posebna slučaja ( A = 0, A = -1, A= +1) preporučujemo da ne koristite formulu (4) , ali koristite druge relacije. Korisno je zapamtiti da su korijeni jednadžbe cos X = 0 date su formulom
X = π / 2 +n π ; (5)
korijeni jednadžbe cos X = -1 date su formulom
X = π + 2m π ; (6)
i konačno, korijeni jednadžbe cos X = 1 date su formulom
X = 2m π ; (7)
U zaključku, napominjemo da su formule (4) , (5), (6) i (7) su tačni samo pod pretpostavkom da je željeni ugao X izraženo u radijanima. Ako je izraženo u stepenima, onda ove formule treba prirodno promijeniti. Dakle, formula (4) treba zamijeniti formulom
X = ± arccos a+ 360° n,
formula (5) formula
X = 90° + 180° n itd.
Zakharova Ljudmila Vladimirovna
MBOU "Srednji" sveobuhvatne škole br. 59" Barnaul
nastavnik matematike
[email protected]
№1 Najjednostavnije trigonometrijske jednadžbe
Cilj: 1. Izvesti formule za rješenja najjednostavnijih trigonometrijskih jednačina oblika sinx =a, cosx=a, tgx=a, ctgx=a;
2. Naučite rješavati jednostavne trigonometrijske jednadžbe koristeći formule.
Oprema: 1) Tablice sa grafovima trigonometrijskih funkcija y= sinx, y=cosx, y=tgx, y=ctgx; 2) Tablica vrijednosti inverznih trigonometrijskih funkcija; 3) Zbirna tabela formula za rješavanje jednostavnih trigonometrijskih jednadžbi.
Plan predavanja:
1 .Izvođenje formula za korijene jednadžbe
a) sinx =a,
b) cosx= a,
c ) tgx= a,
d) ctgx= A.
2 . Usmeni frontalni rad za konsolidaciju primljenih formula.
3 . Pisani rad za konsolidaciju proučenog materijala
Tokom nastave.U algebri, geometriji, fizici i drugim predmetima susrećemo se s raznim problemima čije rješavanje uključuje rješavanje jednačina. Proučavali smo svojstva trigonometrijskih funkcija, pa je prirodno da se okrenemo jednadžbi u kojima je nepoznata sadržana pod predznakom funkcije
definicija: Jednačine oblika sinx = a , cosx= a , tgx= a , ctgx= A nazivaju se najjednostavnijim trigonometrijskim jednadžbama.
Vrlo je važno naučiti rješavati najjednostavnije trigonometrijske jednadžbe, jer se sve metode i tehnike za rješavanje bilo koje trigonometrijske jednadžbe sastoje u tome da se one svode na najjednostavnije.
Počnimo s izvođenjem formula koje “aktivno” rade pri rješavanju trigonometrijskih jednačina.
1.Jednačine oblika sinx = a.
Rešimo jednačinu sinx = a grafički. Da bismo to učinili, u jednom koordinatnom sistemu ćemo konstruisati grafove funkcija y=sinx i y= A.
1) Ako A> 1 i A grijeh x= A nema rješenja, jer prava linija i sinusni val nemaju zajedničkih tačaka.
2) Ako -1a a prelazi sinusni val beskonačno mnogo puta. To znači da je jednačina sinx= a ima beskonačno mnogo rješenja.
Pošto je period sinusa 2 
, zatim da riješimo jednačinu sinx= a dovoljno je pronaći sva rješenja na bilo kojem segmentu dužine 2.
Rješavanje jednadžbe na [-/2; /2] po definiciji arcsinusa x= arcsin a, i na x=-arcsin a. Uzimajući u obzir periodičnost funkcije u=sinx, dobijamo sledeće izraze
x = -arcsin a+2n, n Z.
Obje serije rješenja mogu se kombinirati
X = (-1) n arcsin a+n, nZ.
U sljedeća tri slučaja, radije koriste jednostavnije relacije umjesto opće formule:
Ako A=-1, tada sin x =-1, x=-/2+2n
Ako A=1, tada sin x =1, x =/2+2n
Ako a= 0, tada sin x =0. x = n,
Primjer: Riješite jednačinu sinx =1/2.
Kreirajmo formule za rješenja x=arcsin 1/2+ 2n
X= - arcsin a+2n
Izračunajmo vrijednost arcsin1/2. Zamijenimo pronađenu vrijednost u formule rješenja
x=5/6+2n
ili prema opštoj formuli
X= (-1) n arcsin 1/2+n,
X= (-1) n /6+n,
2. Jednačine oblika cosx= a.
Rešimo jednačinu cosx= a također grafički, crtanjem funkcija y= cosx i y= A.
1) Ako je a 1, onda jednačina cosx= a nema rješenja, jer grafovi nemaju zajedničkih tačaka.
2) Ako je -1 a cosx= a ima beskonačan broj rješenja.
Naći ćemo sva rješenja cosx= a na intervalu dužine 2 pošto je period kosinusa 2.
Prema definiciji arc kosinusa, rješenje jednadžbe će biti x= arcos a. Uzimajući u obzir parnost kosinusne funkcije, rješenje jednadžbe na [-;0] će biti x=-arcos a.
Dakle, rješavanje jednačine cosx= a x= + arcos a+ 2 n,
U tri slučaja nećemo koristiti opću formulu, već jednostavnije relacije:
Ako A=-1, zatim cosx =-1, x =-/2+2n
Ako A=1, tada je cosx =1, x = 2n,
Ako je a=0, onda je cosx=0. x =/2+n
Primjer: Riješite jednačinu cos x =1/2,
Kreirajmo formule za rješenja x=arccos 1/2+ 2n
Izračunajmo vrijednost arccos1/2.
Zamijenimo pronađenu vrijednost u formule rješenja
X= + /3+ 2n, nZ.
Jednačine oblika tgx= a.
Pošto je period tangente jednak, onda da bi se našla sva rješenja jednačine tgx= a, dovoljno je pronaći sva rješenja na bilo kojem intervalu dužine . Po definiciji arktangensa, rješenje jednadžbe na (-/2; /2) je arktan a. Uzimajući u obzir period funkcije, sva rješenja jednadžbe mogu se zapisati u obliku
x= arktan a+ n, nZ.
primjer: Riješite jednačinu tan x = 3/3
Napravimo formulu za rješavanje x= arctan 3/3 +n, nZ.
Izračunajmo vrijednost arktangensa arktan 3/3= /6, onda
X=/6+ n, nZ.
Izvođenje formule za rješavanje jednadžbe With tgx= a može se dati studentima.
Primjer.
Riješite jednačinu ctg x = 1.
x = arcctg 1 + n, nZ,
X = /4 + n, nZ.
Kao rezultat proučenog materijala, učenici mogu popuniti tabelu:
"Rješavanje trigonometrijskih jednadžbi."
jednačina
Vježbe za konsolidaciju proučenog gradiva.
(Usmeno) Koja od napisanih jednačina se može riješiti pomoću formula:
a) x= (-1) n arcsin a+n, nZ;
b) x= + arcos a+ 2n?
cos x = 2/2, tan x= 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3, cos x = 2 .
Koja od sljedećih jednačina nema rješenja?
Riješite jednačine:
a) sin x = 0; e) sin x = 2/2; h) sin x = 2;
b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;
d) tan x = 3; g) dječji krevetić x = -1; j) tan x = 1/3.
3. Riješite jednačine:
a) sin 3x = 0; e) 2cos x = 1;
b) cos x/2 =1/2; e) 3 tg 3x =1;
d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.
Prilikom rješavanja ovih jednačina korisno je zapisati pravila za rješavanje jednačina oblika grijeh V x = a, And With grijeh V x = a, | a|1.
Sin V x = a, |a|1.
V x = (-1) n arcsin a+n, nZ,
x= (-1) n 1/ V arcsin a+n/ V, nZ.
Sumiranje lekcije:
Danas smo na času izvodili formule za rješavanje jednostavnih trigonometrijskih jednadžbi.
Pogledali smo primjere rješavanja jednostavnih trigonometrijskih jednadžbi.
Popunili smo tabelu koju ćemo koristiti za rješavanje jednačina.
Zadaća.
№2 Rješavanje trigonometrijskih jednačina
Cilj: Metode proučavanja za rješavanje trigonometrijskih jednačina: 1) svodive na kvadratne 2) svodljive na homogene trigonometrijske jednačine;
Razvijati sposobnosti zapažanja učenika prilikom upotrebe na razne načine rješavanje trigonometrijskih jednačina.
Frontalni rad sa učenicima.
Koje su formule za korijene trigonometrijskih jednadžbi? cos x= a, sin x= a, tgx = a, ctg x = a.
Riješite jednačine (usmeno):
cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.
Pronađite greške i razmislite o razlozima za greške.
cos x=1/2, x= +
/6+2k,k 
Z.
sin x= 3/2, x= /3+k, kZ.
tgx = /4, x=1+ k, kZ.
2. Proučavanje novog gradiva.
On ovu lekciju Biće reči o nekim od najčešćih metoda za rešavanje trigonometrijskih jednačina.
Trigonometrijske jednadžbe svedene na kvadratne.
Ova klasa može uključivati jednadžbe koje uključuju jednu funkciju (sinus ili kosinus) ili dvije funkcije istog argumenta, ali jedna od njih koristi osnovni trigonometrijskih identiteta svodi se na drugo.
Na primjer, ako cosh uđe u jednačinu u parnim stepenima, onda je zamjenjujemo sa 1-sin 2 x, ako je sin 2 x, onda je zamjenjujemo sa 1-cos 2 x.
Primjer.
Riješi jednačinu: 8 sin 2 x - 6sin x -5 =0.
Rješenje: Označimo sin x=t, zatim 8t 2 - 6t – 5=0,
D= 196,
T 1 = -1/2, t 2 = -5/4.
Izvršimo obrnutu zamjenu i riješimo sljedeće jednačine.
X=(-1) k+1 /6+ k, kZ.
Pošto -5/4>1, jednačina nema korijena.
Odgovor: x=(-1) k+1 /6+ k, kZ.
Rješavanje vježbi konsolidacije.
Riješite jednačinu:
1) 2sin 2 x+ 3cos x = 0;
2) 5sin 2 x+ 6cos x -6 = 0;
3) 2sin 2 x+ 3cos 2 x = -2sin x;
4) 3 tg 2 x +2 tgx-1=0.
Homogene trigonometrijske jednadžbe.
definicija: 1) Jednačina oblikaa sinx + b cosx=0, (a=0, b=0) naziva se homogena jednačina prvog stepena u odnosu na sin x i cos x.
Odlucuje se zadata jednačina dijeljenjem oba dijela sa cosx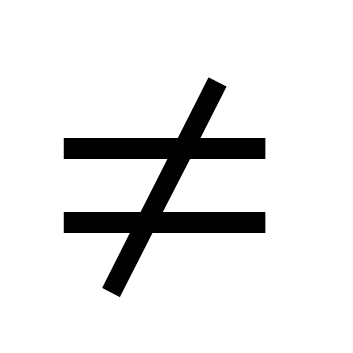 
0. Rezultat je jednačina atgx+ b=0.
2) Jednačina oblikaa grijeh 2 x + b sinx cosx + c cos 2 x =0 naziva se homogena jednačina drugog stepena, gde su a, b, c bilo koji brojevi.
Ako je a = 0, tada rješavamo jednačinu dijeljenjem obje strane sa cos 2 x 0. Kao rezultat, dobijamo jednačinu atg 2 x+ btgx+s =0.
komentar: Jednačina oblikaa grijeh mx + b cos mx=0 ili
a grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx =0 takođe su homogeni. Da bismo ih riješili, obje strane jednačine podijeljene su sa cos mx=0 ili cos 2 mx=0
3) Može se svesti na homogene jednačine razne jednačine, koji u početku nisu takvi. Na primjer,grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx = d, I a sinx + b cosx= d. Da biste riješili ove jednačine, trebate pomnožiti desnu stranu "trigonometrijska jedinica" one. on grijeh 2 x + cos 2 x i izvodi matematičke transformacije.
Vježbe za konsolidaciju proučenog materijala:
1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;
2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;
3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;
4) sin 2 x -3 sinx cosx +2 cos 2 x =0
3. Sumiranje lekcije. Zadaća.
U ovoj lekciji, ovisno o pripremljenosti grupe, možete razmotriti rješavanje jednadžbi oblika a sin mx +b cos mx=c, gdje a, b, c nisu jednaki nuli u isto vrijeme.
Vježbe za jačanje:
1. 3sin x + cos x=2;
2. 3sin 2x + cos 2x= 2;
3. sin x/3 + cos x/3=1;
4. 12 sin x +5 cos x+13=0.
№ 3 Rješavanje trigonometrijskih jednačina
Cilj: 1) Proučiti metodu rješavanja trigonometrijskih jednačina faktorizacijom; naučiti rješavati trigonometrijske jednačine koristeći različite trigonometrijske formule;
2) Provjeriti: znanje učenika o formulama za rješavanje jednostavnih trigonometrijskih jednačina; sposobnost rješavanja jednostavnih trigonometrijskih jednačina.
Plan lekcije:
Provjera domaćeg.
Matematički diktat.
Učenje novog gradiva.
Samostalan rad.
Sumiranje lekcije. Zadaća.
Napredak lekcije:
Provjera domaćeg (rješenja trigonometrijskih jednačina su ukratko napisana na tabli).
Matematički diktat.
U 1
1. Koje se jednačine nazivaju najjednostavnijim trigonometrijskim jednačinama?
2. Kako se zove jednačina oblikaa sinx + b cosx=0? Navedite način da to riješite.
3. Zapišite formulu za korijene jednadžbe tgx = a(ctg x= a).
4. Zapišite formule za korijene jednadžbi oblika cosx= a, Gdje A=1, A=0, A=-1.
5. Zapišite opću formulu za korijene jednadžbe sin x= a, | a|
6. Kako se rješavaju jednačine oblikaa cosx= b, | b|
U 2
1. Zapišite formule za korijene jednadžbi cosx= a,| a|
2. Zapišite opću formulu za korijene jednadžbe
= a, | a|
3. Kako se nazivaju jednačine oblika? sin x= a, tgx = a, sin x= a?
4. Zapišite formule za korijene jednadžbe sin x= a, Ako A=1, A=0, A=-1.
5. Kako se rješavaju jednačine oblika grijeh a x= b, | b|
6. Kako se nazivaju jednačine homogene jednačine drugi stepen? Kako su riješeni?
Učenje novog gradiva.
Metoda faktorizacije.
Jedna od najčešće korišćenih metoda za rešavanje trigonometrijskih jednačina je metoda faktorizacije.
Ako se jednačina f(x) =0 može predstaviti kao f 1 (x) f 2 (x) =0, onda se problem svodi na rješavanje dvije jednadžbe f 1 (x) = 0, f 2 (x) = 0 .
(Kod učenika je korisno zapamtiti pravilo “ Proizvod faktora jednak je nuli ako je barem jedan od faktora jednaka nuli, dok drugi imaju smisla»)
Konsolidacija proučavanog materijala kroz rješavanje jednačina različite složenosti.
(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(self)
3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;
5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 načina)
7) cosx+ cos3x=0; 8) sin 3x= sin 17x;
9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x
11) sin x cos5x = sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x+ cos 2 x=0(self)
13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.
Samostalan rad.
Opcija-1 Opcija-2
1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;
2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;
3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;
4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;
5) sin x+cosx=1. 5) sin x+cosx=2.
8. Sumiranje lekcije. Zadaća.
Centrirano u tački A.
α
- ugao izražen u radijanima.
Definicija
sinus (sin α)- Ovo trigonometrijska funkcija, u zavisnosti od ugla α između hipotenuze i kraka pravouglog trougla, jednakog omjeru dužine suprotne krake |BC| na dužinu hipotenuze |AC|.
kosinus (cos α) je trigonometrijska funkcija koja ovisi o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru dužine susjednog kraka |AB| na dužinu hipotenuze |AC|.
Prihvaćene notacije
;
;
.
;
;
.
Grafikon funkcije sinusa, y = sin x
Grafikon kosinusne funkcije, y = cos x
Svojstva sinusa i kosinusa
Periodičnost
Funkcije y = sin x i y = cos x periodično sa periodom 2π.
Paritet
Funkcija sinusa je neparna. Kosinusna funkcija je parna.
Domen definicije i vrijednosti, ekstremi, povećanje, smanjenje
Sinusne i kosinusne funkcije su kontinuirane u svojoj domeni definicije, odnosno za sve x (vidi dokaz kontinuiteta). Njihova glavna svojstva prikazana su u tabeli (n - cijeli broj).
| y = sin x | y = cos x | |
| Obim i kontinuitet | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| Raspon vrijednosti | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Povećanje | ||
| Silazno | ||
| Maksimum, y = 1 | ||
| Minimum, y = - 1 | ||
| Nule, y = 0 | ||
| Točke preseka sa ordinatnom osom, x = 0 | y = 0 | y = 1 |
Osnovne formule
Zbir kvadrata sinusa i kosinusa
Formule za sinus i kosinus iz zbira i razlike
;
;
Formule za proizvod sinusa i kosinusa
Formule zbira i razlike
Izražavanje sinusa kroz kosinus
;
;
;
.
Izražavanje kosinusa kroz sinus
;
;
;
.
Izraz kroz tangentu
; .
Kada imamo:
;
.
u:
;
.
Tablica sinusa i kosinusa, tangenta i kotangensa
Ova tabela prikazuje vrijednosti sinusa i kosinusa za određene vrijednosti argumenta. 
Izrazi kroz kompleksne varijable
;
Ojlerova formula
Izrazi kroz hiperboličke funkcije
;
;
Derivati
; . Izvođenje formula > > >
Derivati n-tog reda:
{ -∞ <
x < +∞ }
Sekans, kosekans
Inverzne funkcije
Inverzne funkcije sinusa i kosinusa su arksinus i arkosinus, respektivno.
Arcsin, arcsin
Arccosine, arccos
Reference:
I.N. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente, „Lan“, 2009.