Sinx a shaklidagi tenglamalar. Trigonometrik tenglamalarni yechish. Kosinus funksiyasining grafigi, y = cos x

Dars turi: o'quv vazifasini belgilash.

Dars maqsadlari:

Tarbiyaviy: talabalarning oddiy trigonometrik tenglamalarni yechish usullari haqidagi bilimlarini tizimlashtirish, doira va jadvallar bilan ishlash ko‘nikmalarini mustahkamlash.

Rivojlanish: trigonometrik tenglamalarni yechishning turli usullarini qo'llash orqali o'quvchilarning ijodiy intellektual qobiliyatlarini shakllantirish bo'yicha ishlarni davom ettirish.

Tarbiyaviy: jamoaviy aqliy faoliyat ko'nikmalarini rivojlantirish, o'zaro yordam va o'z nuqtai nazaridan farqli nuqtai nazarni qabul qilish.

Darslar davomida

1. Muvaffaqiyat holati.

Tenglamani yeching: cosx=1; cosx=0; cosx= -1.

2. Bilim va jaholat o‘rtasidagi vaziyat, bo‘shliq”.

Tenglamani yeching: cosx=½; cosx=a.

Munozara.

3. Tarbiyaviy vazifa bayoni.

Bunday turdagi tenglamani qanday yechish mumkin?

1) (1;0) nuqtani koordinata aylanasi atrofidagi burchakka teng burchak bilan aylantirganda olingan birlik aylanadagi nuqtaning abssissasi nimaga teng: ?

2). Nimaga teng: ?

Javob:

3).Qandayga teng: .

Javob:

;

;

(1) .

O'qituvchining so'zi: matematiklar teskari cos so'zlarini arkkosin (arccos) so'zi deb atashgan. Raqamning yoyi kosinusi kosinasi a ga teng bo'lgan sondir:
arccosa=a, agar cosa=a va 0≤a≤p boʻlsa.

4). Arccos belgisi yordamida tenglikni (1) yozing.

5). Tenglamalarni yeching: cosx=½, cosx=a.

Javob: x=arccos½, x=arccosa.

6). Abtsissasi ½ ga teng bo'lgan birlik doiraning (1;0) nuqtasining burilish burchaklarini ayting.

Javob: nuqta p/3 va -p/3 ga teng burchak bilan aylantirilganda abtsissa ½ ga teng.

ya'ni cosx=½ da x=±arccos½
cosx=a da x=±arkkosa.

7). (1;0) nuqtani burchaklar bilan burish natijasida olingan nuqtalarning abssissalari nimaga teng: p/3+2p; p/3+6p; -p/3+4p; -p/3+8p; p/3+2pn; -p/3+2pn.

Javob: abscissa ½ ga teng va x=±arccos½+2pn, da cosx=½.
cosx=a da x=±arccosa+2pn,.

8). Xulosa: cosx=a tenglama

1) agar ≤1 bo'lsa, ildizlari bor,
2) agar >1 boʻlsa, ildizlari yoʻq.

9). Dars xulosasi:

a) a va a ning qaysi qiymatlari uchun arccosa = a tengligi ma'noga ega?
b) a ning yoy kosinusu nima deyiladi?
c) cosx=a tenglama a ning qaysi qiymatlarida ildizlarga ega?
d) cosx=a tenglamaning ildizlarini topish formulasi.

Misollar:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

Trigonometrik tenglamalarni yechish usullari:

Har qanday trigonometrik tenglama quyidagi turlardan biriga qisqartirilishi kerak:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

Bu erda \(t\) - x bilan ifodalangan, \(a\) - son. Bunday trigonometrik tenglamalar chaqiriladi eng oddiy. Ularni () yoki maxsus formulalar yordamida osongina echish mumkin:

Oddiy trigonometrik tenglamalarni yechish bo'yicha infografikaga qarang:, va.

Misol . \(\sin⁡x=-\)\(\frac(1)(2)\) trigonometrik tenglamani yeching.
Yechim:

Javob: \(\left[ \begin(to'plangan)x=-\frac(p)(6)+2pk, \\ x=-\frac(5p)(6)+2pn, \end(to'plangan)\o'ng.\) \(k,n∈Z\)

Trigonometrik tenglamalarning ildizlari formulasida har bir belgi nimani anglatadi, qarang.

Diqqat!\(\sin⁡x=a\) va \(\cos⁡x=a\) tenglamalarining yechimlari yo'q, agar \(a s (-∞;-1)∪(1;∞)\). Chunki har qanday x uchun sinus va kosinus \(-1\) dan katta yoki teng va \(1\) dan kichik yoki teng:

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

Misol . \(\cos⁡x=-1,1\) tenglamasini yeching.
Yechim: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Javob : yechim yo'q.

Misol . tg\(⁡x=1\) trigonometrik tenglamani yeching.
Yechim:

Raqamli aylana yordamida tenglamani yechamiz. Buning uchun: 1) Doira qurish) 2) \(x\) va \(y\) o'qlarini va teginish o'qini (u \(y\) o'qiga parallel \((0;1)\) nuqtadan o'tadi) tuzing. 3) Tangens o'qida \(1\) nuqtani belgilang. 4) Ushbu nuqtani va koordinatalarning boshini - to'g'ri chiziq bilan bog'lang. 5) Bu chiziq va sonli doiraning kesishish nuqtalarini belgilang. 6) Keling, ushbu nuqtalarning qiymatlarini belgilaymiz: \(\frac(p)(4)\) ,\(\frac(5p)(4)\) 7) Ushbu nuqtalarning barcha qiymatlarini yozing. Ular bir-biridan aniq \(p\) masofada joylashganligi sababli, barcha qiymatlarni bitta formulada yozish mumkin:

Javob: \(x=\)\(\frac(p)(4)\) \(+pk\), \(k∈Z\).

Misol . \(\cos⁡(3x+\frac(p)(4))=0\) trigonometrik tenglamani yeching.
Yechim:

Keling, yana raqam doirasini ishlatamiz. 1) Doira, o'qlarni \(x\) va \(y\) qurish. 2) Kosinus o'qida (\(x\) o'qi) \(0\) belgilang. 3) Shu nuqta orqali kosinus o‘qiga perpendikulyar chizamiz. 4) Perpendikulyar va aylananing kesishish nuqtalarini belgilang. 5) Keling, ushbu nuqtalarning qiymatlarini belgilaymiz: \(-\) \(\frac(p)(2)\),\(\frac(p)(2)\). 6) Biz bu nuqtalarning butun qiymatini yozamiz va ularni kosinusga (kosinus ichidagi narsaga) tenglashtiramiz. \(3x+\)\(\frac(p)(4)\) \(=±\)\(\frac(p)(2)\) \(+2pk\), \(k∈Z\) \(3x+\)\(\frac(p)(4)\) \(=\)\(\frac(p)(2)\) \(+2pk\) \(3x+\)\(\frac( p)(4)\) \(=-\)\(\frac(p)(2)\) \(+2pk\) 8) Odatdagidek \(x\) ni tenglamalarda ifodalaymiz. Raqamlarga \(p\), shuningdek \(1\), \(2\), \(\frac(1)(4)\) va boshqalar bilan ishlov berishni unutmang. Bu boshqa barcha raqamlar bilan bir xil raqamlar. Raqamli kamsitish yo'q! \(3x=-\)\(\frac(p)(4)\) \(+\)\(\frac(p)(2)\) \(+2pk\) \(3x=-\)\ (\frac(p)(4)\) \(+\)\(\frac(p)(2)\) \(+2pk\) \(3x=\)\(\frac(p)(4)\) \(+2pk\) \(|:3\) \(3x=-\)\(\frac(3p)(4)\) \(+2pk\) \(|:3\) \(x=\)\(\frac(p)(12)\) \(+\)\(\frac(2pk)(3)\) \(x=-\)\(\frac(p)( 4)\) \(+\)\(\frac(2pk)(3)\)

Javob: \(x=\)\(\frac(p)(12)\) \(+\)\(\frac(2pk)(3)\) \(x=-\)\(\frac(p)( 4)\) \(+\)\(\frac(2pk)(3)\) , \(k∈Z\).

Trigonometrik tenglamalarni eng sodda qilib qisqartirish - bu erda siz tenglamalarni echish uchun ikkala va maxsus usullardan foydalanishingiz kerak:
- Usul (Yagona davlat imtihonida eng mashhur).
- Usul.
- Yordamchi argumentlar usuli.

Kvadrat trigonometrik tenglamani yechish misolini ko‘rib chiqamiz

Misol . \(2\cos^2⁡x-5\cos⁡x+2=0\) trigonometrik tenglamani yeching.
Yechim:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	Keling, \(t=\cos⁡x\) almashtirishni amalga oshiramiz.
	Bizning tenglamamiz odatiy holga aylandi. dan foydalanib hal qilishingiz mumkin.
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	Biz teskari almashtirishni amalga oshiramiz.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	Birinchi tenglamani sonli aylana yordamida yechamiz. Ikkinchi tenglamaning yechimlari yo'q, chunki \(\cos⁡x∈[-1;1]\) va har qanday x uchun ikkitaga teng bo'lishi mumkin emas.
	Keling, ushbu nuqtalarda yotgan barcha raqamlarni yozamiz.

Javob: \(x=±\)\(\frac(p)(3)\) \(+2pk\), \(k∈Z\).

ODZni o'rganish bilan trigonometrik tenglamani yechish misoli:

Misol (FOYDALANISH) . \(=0\) trigonometrik tenglamani yeching.

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Kasr bor va kotangent bor - bu biz uni yozishimiz kerakligini anglatadi. Sizga shuni eslatib o'tamanki, kotangent aslida kasrdir: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) Shuning uchun ctg\(x\) uchun ODZ: \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(p)(2)\) \(+2pk\); \(x≠pn\); \(k,n∈Z\)	Raqamlar doirasiga "yechim bo'lmagan" ni belgilaymiz.
\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Keling, tenglamadagi maxrajni ctg\(x\) ga ko'paytirish orqali qutulamiz. Biz buni qila olamiz, chunki biz yuqorida ctg\(x ≠0\) deb yozgan edik.
\(2\cos^2⁡x-\sin⁡(2x)=0\)	Sinus uchun ikki tomonlama burchak formulasini qo'llaymiz: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	Agar qo'llaringiz kosinusga bo'linish uchun cho'zilsa, ularni orqaga torting! Oʻzgaruvchiga ega ifodaga boʻlish mumkin, agar u aniq nolga teng boʻlmasa (masalan, bular: \(x^2+1.5^x\)). Buning o'rniga, qavs ichidan \(\cos⁡x\) ni qo'yamiz.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	Keling, tenglamani ikkiga "bo'laylik".
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	Birinchi tenglamani sonli aylana yordamida yechamiz. Ikkinchi tenglamani \(2\) ga bo'lib, \(\sin⁡x\) ni o'ng tomonga o'tkazamiz.
\(x=±\)\(\frac(p)(2)\) \(+2pk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	Olingan ildizlar ODZga kiritilmaydi. Shuning uchun biz ularni javob sifatida yozmaymiz. Ikkinchi tenglama odatiy hisoblanadi. Keling, uni \(\sin⁡x\) ga bo'laylik (\(\sin⁡x=0\) tenglamaning yechimi bo'la olmaydi, chunki bu holda \(\cos⁡x=1\) yoki \(\cos⁡) x=-1\)).
	Biz yana aylanadan foydalanamiz.
\(x=\)\(\frac(p)(4)\) \(+pn\), \(n∈Z\)	Bu ildizlar ODZ tomonidan chiqarib tashlanmaydi, shuning uchun ularni javobda yozishingiz mumkin.

Javob: \(x=\)\(\frac(p)(4)\) \(+pn\), \(n∈Z\).

cos tenglamasi X = A

Tenglamaning har bir ildizi

cos X = A (1)

sinusoidning ayrim kesishish nuqtasining abssissasi sifatida qaralishi mumkin y = cosX to'g'ri chiziq bilan y =A , va aksincha, har bir bunday kesishish nuqtasining abscissasi (1) tenglamaning ildizlaridan biridir. y = cosX to'g'ri chiziq bilan y = A .

Agar | A| >1 , keyin kosinus y = cosX chiziq bilan kesishmaydi y = A .

Bu holda (1) tenglamaning ildizlari yo'q.

Da |A| < 1 cheksiz ko'p kesishish nuqtalari mavjud.

a > 0 uchun

a uchun< 0.

Biz barcha kesishgan nuqtalarni ikki guruhga ajratamiz:

A -2 , A - 1 , A 1 , A 2 , ... ,

B -2 , B - 1 , B 1 , B 2 , ... ,

Nuqta A abtsissaga ega arccos A , va birinchi guruhning boshqa barcha nuqtalari undan 2 ga karrali masofalarda ajratiladi π

arccos a+ 2k π . (2)

Nuqta IN, raqamlardan osonlik bilan tushunish mumkinki, abscissaga ega - arkkosA , va ikkinchi guruhning barcha boshqa nuqtalari undan 2 ga karrali masofalarda chiqariladi π . Shuning uchun ularning abstsissalari quyidagicha ifodalanadi

arccos A+ 2nπ . (3)

Shunday qilib, (1) tenglama (2) va (3) formulalar bilan aniqlangan ikkita ildiz guruhiga ega. Ammo bu ikki formulani bitta formula sifatida yozish mumkin

X = ± arkkos a+ 2 m π , (4)

Qayerda m barcha butun sonlar (m = 0, ±1, ±2, ±3, ...) orqali ishlaydi.

Ushbu formulani chiqarishda biz qilgan mulohaza faqat agar to'g'ri bo'lsa
| a| =/= 1. Biroq, rasmiy munosabat (4) tenglamaning barcha ildizlarini aniqlaydi cosx=a va | da A| =1. (Isbotlang!) Shuning uchun formulani aytishimiz mumkin (4) har qanday qiymatlar uchun (1) tenglamaning barcha ildizlarini beradi A , Agarda |A| < 1 .

Ammo uchta alohida holatda ( A = 0, A = -1, A= +1) formuladan foydalanmaslikni tavsiya qilamiz (4) , lekin boshqa munosabatlardan foydalaning. Tenglamaning ildizlari ekanligini eslash foydalidir cos X = 0 formula bilan beriladi

X = π / 2 +n π ; (5)

tenglamaning ildizlari cos X = -1 formula bilan beriladi

X = π + 2 m π ; (6)

va nihoyat, tenglamaning ildizlari cos X = 1 formula bilan beriladi

X = 2m π ; (7)

Xulosa qilib shuni ta'kidlaymizki, formulalar (4) , (5), (6) va (7) faqat kerakli burchak degan faraz ostida to'g'ri X radianlarda ifodalanadi. Agar u darajalarda ifodalangan bo'lsa, unda bu formulalarni tabiiy ravishda o'zgartirish kerak. Shunday qilib, formula (4) formula bilan almashtirilishi kerak

X = ± arkkos a+ 360° n,

formula (5) formulasi

X = 90° + 180° n va hokazo.

Zaxarova Lyudmila Vladimirovna
MBOU "Ikkilamchi" umumta'lim maktabi№ 59" Barnaul
matematika o'qituvchisi [elektron pochta himoyalangan]

№1 Eng oddiy trigonometrik tenglamalar

Maqsad: 1. Shakldagi eng oddiy trigonometrik tenglamalar yechimlari formulalarini chiqaring sinx =a, cosx=a, tgx=a, ctgx=a;

2. Oddiy trigonometrik tenglamalarni formulalar yordamida yechishni o‘rganing.

Uskunalar: 1) y= trigonometrik funksiyalar grafiklari bilan jadvallar sinx, y=cosx, y=tgx, y=ctgx; 2) Teskari trigonometrik funktsiyalar qiymatlari jadvali; 3) Oddiy trigonometrik tenglamalarni yechish uchun formulalar jadvali.

Ma'ruza dars rejasi:

1 .Tenglama ildizlari uchun formulalar hosil qilish

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= A.

2 . Qabul qilingan formulalarni mustahkamlash uchun og'zaki frontal ish.

3 . O'rganilgan materialni mustahkamlash uchun yozma ish

Darslar davomida.

Algebra, geometriya, fizika va boshqa fanlarda biz turli xil muammolarga duch kelamiz, ularning yechimi tenglamalarni echishni o'z ichiga oladi. Biz trigonometrik funktsiyalarning xususiyatlarini o'rganib chiqdik, shuning uchun noma'lum funktsiya belgisi ostida joylashgan tenglamalarga murojaat qilish tabiiydir.

Ta'rif: Shakl tenglamalari sinx = a , cosx= a , tgx= a , ctgx= A eng oddiy trigonometrik tenglamalar deyiladi.

Eng oddiy trigonometrik tenglamalarni echishni o'rganish juda muhim, chunki har qanday trigonometrik tenglamalarni echishning barcha usullari va usullari ularni eng oddiyiga qisqartirishdan iborat.

Keling, trigonometrik tenglamalarni yechishda “faol” ishlaydigan formulalarni chiqarishdan boshlaylik.

1.Sinx = ko'rinishdagi tenglamalar a.

Sinx = tenglamasini yechamiz a grafik jihatdan. Buning uchun bitta koordinatalar tizimida y=sinx va y= funksiyalarning grafiklarini tuzamiz. A.

1) Agar A> 1 va A gunoh x= A yechimlari yo'q, chunki to'g'ri chiziq va sinus to'lqinning umumiy nuqtalari yo'q.

2) Agar -1a a sinus to'lqinni cheksiz ko'p marta kesib o'tsa. Bu tenglamani anglatadi sinx = a cheksiz ko'p echimlarga ega.

Chunki sinus davri 2 ga teng , keyin tenglamani yechish uchun sinx = a 2 uzunlikdagi istalgan segmentdagi barcha yechimlarni topish kifoya.

[-/2 dagi tenglamani yechish; /2] arksinus x= taʼrifi boʻyicha arcsin a, va x=-arcsin da a. u=sinx funksiyaning davriyligini hisobga olib, quyidagi ifodalarni olamiz

x = -arksin a+2n, n Z.

Ikkala seriyali echimlar birlashtirilishi mumkin

X = (-1) n arksin a+n, nZ.

Quyidagi uchta holatda ular umumiy formuladan ko'ra oddiyroq munosabatlardan foydalanishni afzal ko'radilar:

Agar A=-1, keyin sin x =-1, x=-/2+2n

Agar A=1, keyin sin x =1, x =/2+2n

Agar a= 0, keyin sin x =0. x = n,

Misol: Tenglamani yechish sinx = 1/2.

Yechimlar uchun formulalar tuzamiz x=arksin 1/2+ 2n

X= - yoy a+2n

Keling, qiymatni hisoblaylik arcsin1/2. Topilgan qiymatni yechim formulalariga almashtiramiz

x=5/6+2n

yoki umumiy formula bo'yicha

X= (-1) n arksin 1/2+n,

X= (-1) n /6+n,

2. Shaklning tenglamalari cosx = a.

cosx= tenglamani yechamiz a y= cosx va y= funksiyalarining grafigini grafik jihatdan ham A.

1) Agar 1 bo'lsa, tenglama cosx = a ning yechimlari yo'q, chunki grafiklarning umumiy nuqtalari yo'q.

2) -1 bo'lsa a cosx = a cheksiz sonli yechimlarga ega.

Biz barcha echimlarni topamiz cosx = a kosinus davri 2 ga teng bo'lgani uchun 2 uzunlik oralig'ida.

Yoy kosinusining ta'rifiga ko'ra, tenglamaning yechimi x= bo'ladi arcos a. Kosinus funksiyasining paritetini hisobga olsak, [-;0] dagi tenglamaning yechimi x=-arcos bo'ladi. a.

Shunday qilib, tenglamani yechish cosx = a x= + arcos a+ 2 n,

Uchta holatda biz umumiy formuladan emas, balki oddiyroq munosabatlardan foydalanamiz:

Agar A=-1, keyin cosx =-1, x =-/2+2n

Agar A=1, keyin cosx =1, x = 2n,

Agar a=0 boʻlsa, cosx=0. x =/2+n

Misol: Tenglamani yechish cos x =1/2,

Yechimlar uchun formulalar tuzamiz x=arccos 1/2+ 2n

Keling, qiymatni hisoblaylik arccos1/2.

Topilgan qiymatni yechim formulalariga almashtiramiz

X= + /3+ 2n, nZ.

Shakl tenglamalari tgx= a.

Tangens davri teng bo'lganligi sababli, tenglamaning barcha echimlarini topish uchun tgx= a, har qanday uzunlik oralig'ida barcha echimlarni topish kifoya. Arktangentning ta'rifiga ko'ra, (-/2; /2) bo'yicha tenglamaning yechimi arktandir. a. Funksiya davrini hisobga olgan holda tenglamaning barcha yechimlarini ko’rinishda yozish mumkin

x= arktan a+ n, nZ.

Misol: Tenglamani yeching tan x = 3/3

X= ni yechish formulasini tuzamiz arktan 3/3 +n, nZ.

Arktangens qiymatini hisoblaymiz arktan 3/3= /6, keyin

X=/6+ n, nZ.

Tenglamani yechish formulasini chiqarish Bilan tgx= a talabalarga berilishi mumkin.

Misol.

Tenglamani yeching ctg x = 1.

x = arcstg 1 + n, nZ,

X = /4 + n, nZ.

O'rganilgan material natijasida talabalar jadvalni to'ldirishlari mumkin:

“Trigonometrik tenglamalarni yechish”.

tenglama

O'rganilgan materialni mustahkamlash uchun mashqlar.

(Og'zaki) Yozma tenglamalardan qaysi birini formulalar yordamida yechish mumkin:

a) x= (-1) n arksin a+n, nZ;

b) x= + arcos a+ 2n?

cos x = 2/2, tan x= 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3, cos x = 2 .

Quyidagi tenglamalardan qaysi biri yechimga ega emas?

Tenglamalarni yeching:

a) sin x = 0; e) sin x = 2/2; h) sin x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) tan x = 3; g) krovat x = -1; j) tan x = 1/ 3.

3. Tenglamalarni yeching:

a) sin 3x = 0; e) 2cos x = 1;

b) cos x/2 =1/2; e) 3 tg 3x =1;

d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.

Bu tenglamalarni yechishda ko`rinishdagi tenglamalarni yechish qoidalarini yozib qo`yish maqsadga muvofiqdir gunoh V x = a, Va Bilan gunoh V x = a, | a|1.

Gunoh V x = a, |a|1.

V x = (-1) n arksin a+n, nZ,

x= (-1) n 1/ V arcsin a+n/ V, nZ.

Darsni yakunlash:

Bugun sinfda biz oddiy trigonometrik tenglamalarni yechish uchun formulalar oldik.

Biz oddiy trigonometrik tenglamalarni yechish misollarini ko'rib chiqdik.

Biz tenglamalarni echishda foydalanadigan jadvalni to'ldirdik.

Uy vazifasi.

№2 Trigonometrik tenglamalarni yechish

Maqsad: Trigonometrik tenglamalarni yechishning o'rganish usullari: 1) kvadratga qaytariladigan 2) bir jinsli trigonometrik tenglamalar;

Foydalanishda o'quvchilarning kuzatish ko'nikmalarini rivojlantirish turli yo'llar bilan trigonometrik tenglamalarni yechish.

Talabalar bilan frontal ish.

Trigonometrik tenglamalarning ildizlari uchun qanday formulalar mavjud? cos x= a, sin x= a, tgx = a, ctg x = a.

Tenglamalarni yeching (og'zaki):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.

Xatolarni toping va xatolar sabablari haqida o'ylang.

cos x=1/2, x= + /6+2k,k Z.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. Yangi materialni o'rganish.

Yoniq bu dars Trigonometrik tenglamalarni yechishning eng keng tarqalgan usullaridan ba'zilari ko'rib chiqiladi.

Trigonometrik tenglamalar kvadratga keltirildi.

Bu sinf bir funktsiyani (sinus yoki kosinus) yoki bir xil argumentning ikkita funktsiyasini o'z ichiga olgan tenglamalarni o'z ichiga olishi mumkin, lekin ulardan biri asosiy funktsiyadan foydalanadi. trigonometrik identifikatsiyalar ikkinchi darajaga tushadi.

Masalan, agar cosx tenglamani juft darajalarda kiritsa, uni 1-sin 2 x bilan almashtiramiz, agar sin 2 x bo'lsa, uni 1-cos 2 x bilan almashtiramiz.

Misol.

Tenglamani yeching: 8 sin 2 x - 6sin x -5 =0.

Yechish: belgilaymiz sin x=t, keyin 8t 2 - 6t – 5=0,

D= 196,

T 1 = -1/2, t 2 = -5/4.

Teskari almashtirishni bajaramiz va quyidagi tenglamalarni yechamiz.

X=(-1) k+1 /6+ k, kZ.

-5/4>1 bo'lgani uchun tenglamaning ildizlari yo'q.

Javob: x=(-1) k+1 /6+ k, kZ.

Mustahkamlash mashqlarini yechish.

Tenglamani yeching:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

Bir jinsli trigonometrik tenglamalar.

Ta'rif: 1) Shaklning tenglamasia sinx + b cosx=0, (a=0, b=0) sin x va cos x ga nisbatan birinchi darajali bir jinsli tenglama deyiladi.

Qaror qabul qilinmoqda berilgan tenglama ikkala qismga bo'lish orqali cosx 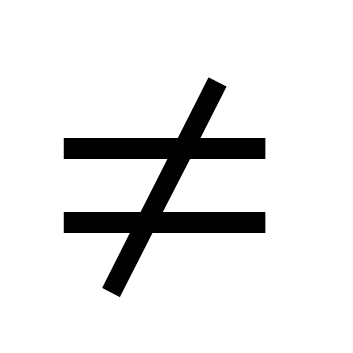0. Natijada tenglama hosil bo'ladi atgx+ b=0.

2) Shaklning tenglamasia gunoh 2 x + b sinx cosx + c cos 2 x =0 ikkinchi darajali bir jinsli tenglama deyiladi, bu erda a, b, c har qanday sonlar.

Agar a = 0 bo'lsa, tenglamani ikkala tomonni bo'lish orqali yechamiz chunki 2 x 0. Natijada tenglamani olamiz atg 2 x+ btgx+s =0.

Izoh: Shakl tenglamasia gunoh mx + b cos mx=0 yoki

a gunoh 2 mx + b gunoh mx cos mx + c cos 2 mx =0 ham bir hildir. Ularni yechish uchun tenglamaning ikkala tomoni cos ga bo'linadi mx=0 yoki cos 2 mx=0

3) Bir jinsli tenglamalarga keltirish mumkin turli tenglamalar, dastlab bunday bo'lmagan. Masalan,gunoh 2 mx + b gunoh mx cos mx + c cos 2 mx = d, Va a sinx + b cosx= d. Ushbu tenglamalarni yechish uchun siz o'ng tomonni ko'paytirishingiz kerak "trigonometrik birlik" bular. yoqilgan gunoh 2 x + cos 2 x va matematik o'zgarishlarni amalga oshirish.

O'rganilgan materialni mustahkamlash uchun mashqlar:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Darsni yakunlash. Uy vazifasi.

Ushbu darsda, guruhning tayyorgarligiga qarab, siz shakldagi tenglamalarni echishni ko'rib chiqishingiz mumkin a sin mx +b cos mx=c, bu erda a, b, c bir vaqtning o'zida nolga teng emas.

Mustahkamlash mashqlari:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 Trigonometrik tenglamalarni yechish

Maqsad: 1) Trigonometrik tenglamalarni koeffitsientlarga ajratish yo‘li bilan yechish usulini o‘rganish; trigonometrik tenglamalarni turli trigonometrik formulalar yordamida yechishni o‘rganish;

2) Tekshirish: talabalarning oddiy trigonometrik tenglamalarni yechish formulalari haqidagi bilimlarini; oddiy trigonometrik tenglamalarni yechish qobiliyati.

Dars rejasi:

Uy vazifasini tekshirish.

Matematik diktant.

Yangi materialni o'rganish.

Mustaqil ish.

Darsni yakunlash. Uy vazifasi.

Darsning borishi:

Uy vazifasini tekshirish (Trigonometrik tenglamalar yechimlari doskaga qisqacha yoziladi).

Matematik diktant.

IN 1

1. Qanday tenglamalar eng oddiy trigonometrik tenglamalar deb ataladi?

2. Shaklning tenglamasi qanday nomlanadia sinx + b cosx=0? Uni hal qilish yo'lini ko'rsating.

3.Tenglamaning ildizlari formulasini yozing tgx = a(ctg x = a).

4. Shakl tenglamalarining ildizlari formulalarini yozing cosx = a, Qayerda A=1, A=0, A=-1.

5. Tenglama ildizlarining umumiy formulasini yozing gunoh x= a, | a|

6. Shaklning tenglamalari qanday echiladia cosx = b, | b|

AT 2

1. Tenglamalarning ildizlari uchun formulalarni yozing cosx = a,| a|

2. Tenglama ildizlarining umumiy formulasini yozing

= a, | a|

3. Ko‘rinishdagi tenglamalar nima deyiladi? gunoh x= a, tgx = a, gunoh x= a?

4.Tenglama ildizlari formulalarini yozing gunoh x= a, Agar A=1, A=0, A=-1.

5. Shaklning tenglamalari qanday echiladi gunoh a x= b, | b|

6. Qanday tenglamalar deyiladi bir jinsli tenglamalar ikkinchi darajali? Ular qanday hal qilinadi?

Yangi materialni o'rganish.

Faktorizatsiya usuli.

Trigonometrik tenglamalarni yechishda eng ko'p qo'llaniladigan usullardan biri bu faktorizatsiya usulidir.

Agar f(x) =0 tenglamani f 1 (x) f 2 (x) =0 ko‘rinishida ifodalash mumkin bo‘lsa, u holda masala ikkita f 1 (x) = 0, f 2 (x) = 0 tenglamalarni yechishga keltiriladi. .

(Talabalar bilan qoidani eslab qolish foydalidir " Faktorlardan kamida bittasi bo'lsa, omillar mahsuloti nolga teng nolga teng, boshqalar esa mantiqiy»)

Turli murakkablikdagi tenglamalarni yechish orqali o‘rganilayotgan materialni mustahkamlash.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(self)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 usul)

7) cosx+ cos3x=0; 8) gunoh 3x = gunoh 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0(self)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Mustaqil ish.

Variant-1 Variant-2

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) gunoh x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. Darsni yakunlash. Uy vazifasi.

Bir nuqtada markazlashtirilgan A.
α - radianlarda ifodalangan burchak.

Ta'rif
Sinus (sin a)- Bu trigonometrik funktsiya, gipotenuza va to'g'ri burchakli uchburchakning oyoqlari orasidagi a burchakka qarab, qarama-qarshi oyoq uzunligining nisbatiga teng |BC| gipotenuzaning uzunligiga |AC|.

Kosinus (cos a) gipotenuza va to‘g‘ri burchakli uchburchakning oyog‘i orasidagi a burchakka bog‘liq bo‘lgan trigonometrik funksiya bo‘lib, qo‘shni oyoq uzunligining nisbatiga teng |AB| gipotenuzaning uzunligiga |AC|.

Qabul qilingan belgilar

;
;
.

;
;
.

Sinus funksiya grafigi, y = sin x

Kosinus funksiyasining grafigi, y = cos x

Sinus va kosinusning xossalari

Davriylik

Funktsiyalar y = gunoh x va y = chunki x davr bilan davriy 2p.

Paritet

Sinus funktsiyasi g'alati. Kosinus funksiyasi juft.

Ta'rif va qadriyatlar sohasi, ekstremal, o'sish, pasayish

Sinus va kosinus funktsiyalari o'z ta'rif sohalarida uzluksizdir, ya'ni barcha x uchun (uzluksizlik isbotiga qarang). Ularning asosiy xossalari jadvalda keltirilgan (n - butun son).

	y = gunoh x	y = chunki x
Qamrov va davomiylik	- ∞ < x < + ∞	- ∞ < x < + ∞
Qiymatlar diapazoni	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Ortib bormoqda
Pastga
Maksim, y = 1
Minimum, y = - 1
Nollar, y = 0
Ordinata o'qi bilan kesishgan nuqtalar, x = 0	y = 0	y = 1

Asosiy formulalar

Sinus va kosinus kvadratlarining yig'indisi

Yig'indi va farqdan sinus va kosinus formulalari

;
;

Sinuslar va kosinuslar hosilasi uchun formulalar

Yig'indi va ayirma formulalari

Kosinus orqali sinusni ifodalash

;
;
;
.

Kosinusni sinus orqali ifodalash

;
;
;
.

Tangens orqali ifodalash

; .

Qachon, bizda:
; .

Da :
; .

Sinuslar va kosinuslar, tangenslar va kotangentlar jadvali

Ushbu jadvalda argumentning ma'lum qiymatlari uchun sinuslar va kosinuslar qiymatlari ko'rsatilgan.

Murakkab o'zgaruvchilar orqali ifodalar

;

Eyler formulasi

Giperbolik funksiyalar orqali ifodalar

;
;

Hosilalar

; . Formulalarni chiqarish > > >

n-tartibli hosilalar:
{ -∞ < x < +∞ }

Sekant, kosekant

Teskari funksiyalar

Sinus va kosinusning teskari funksiyalari mos ravishda arksinus va arkkosindir.

Arksin, arksin

Arkkosin, arkkos

Adabiyotlar:
I.N. Bronshteyn, K.A. Semendyaev, muhandislar va kollej talabalari uchun matematika bo'yicha qo'llanma, "Lan", 2009 yil.